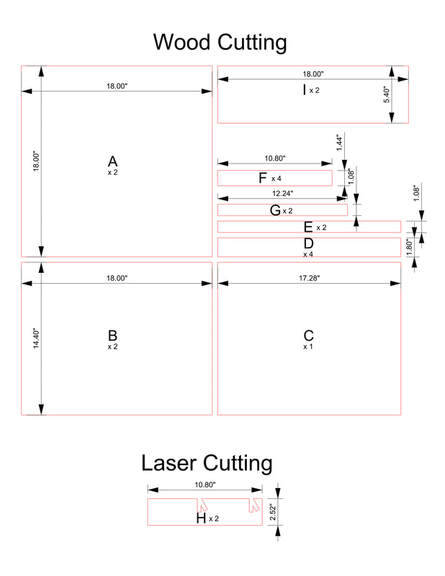
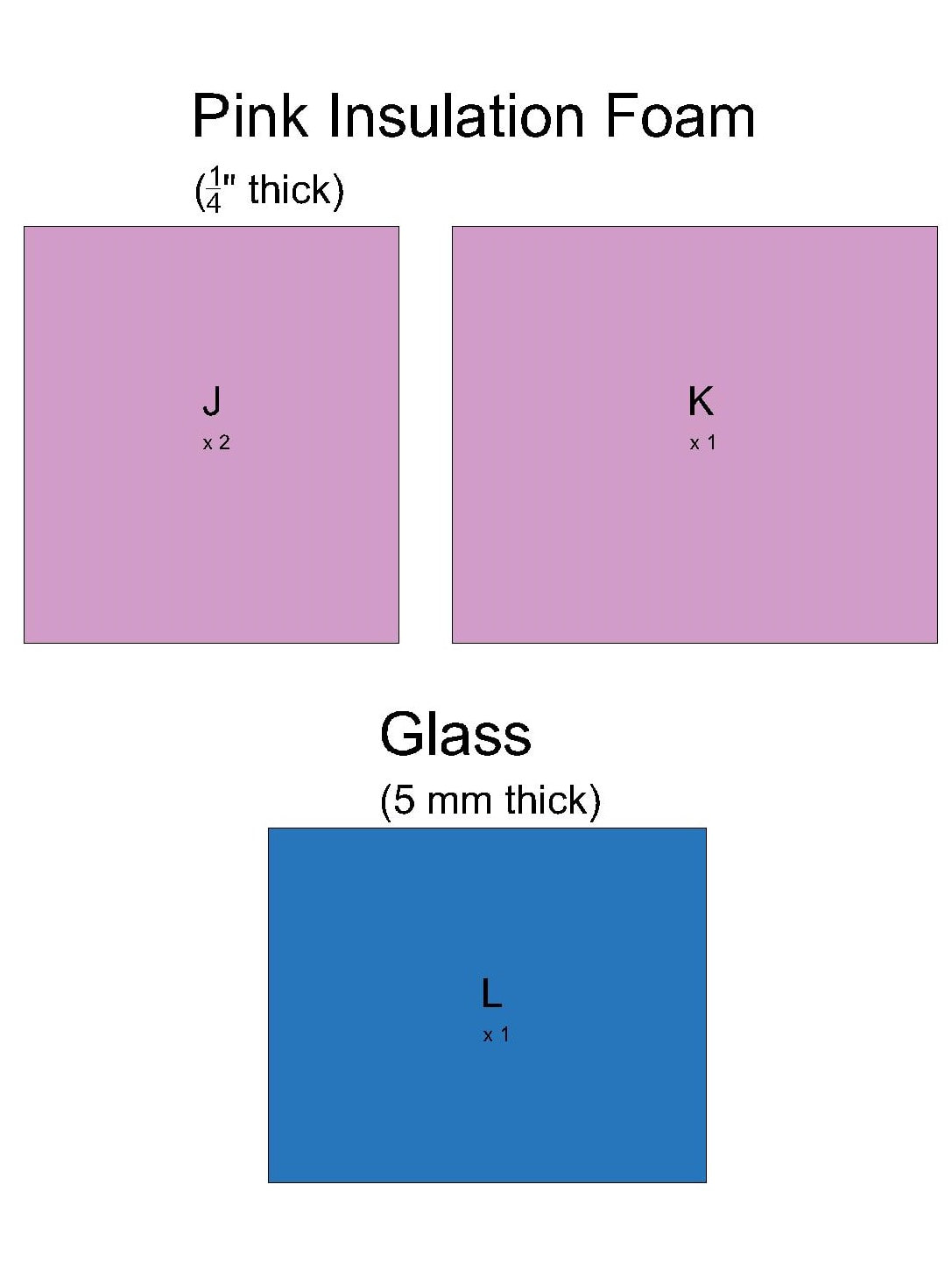
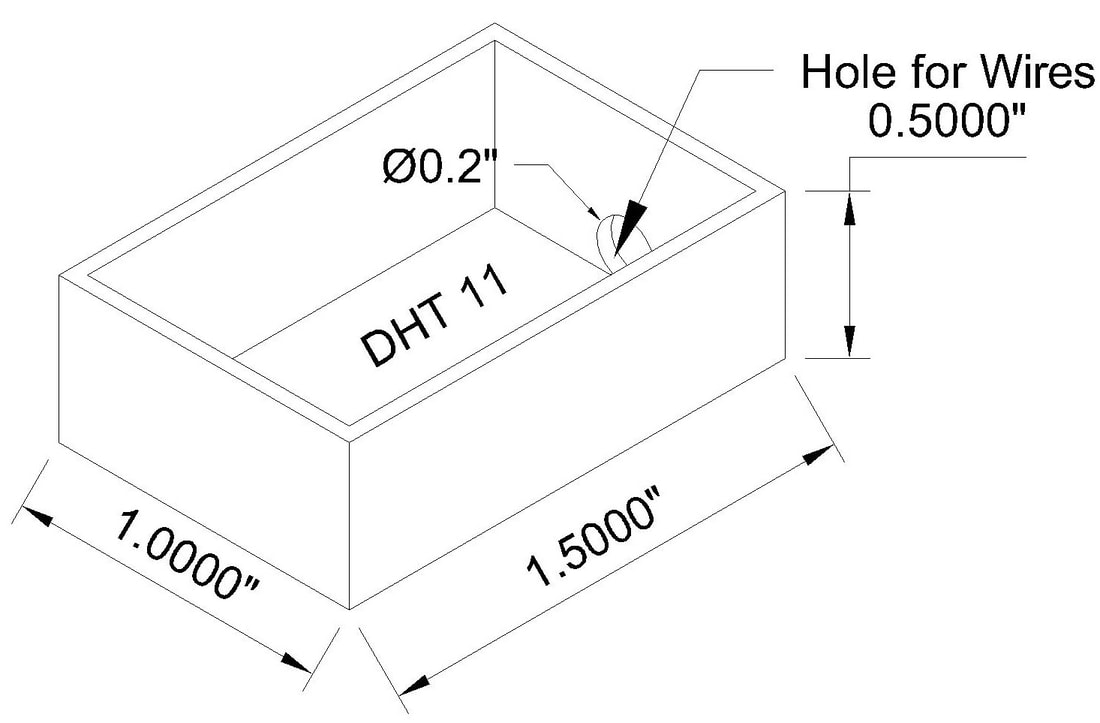
Materials

Process to build the box

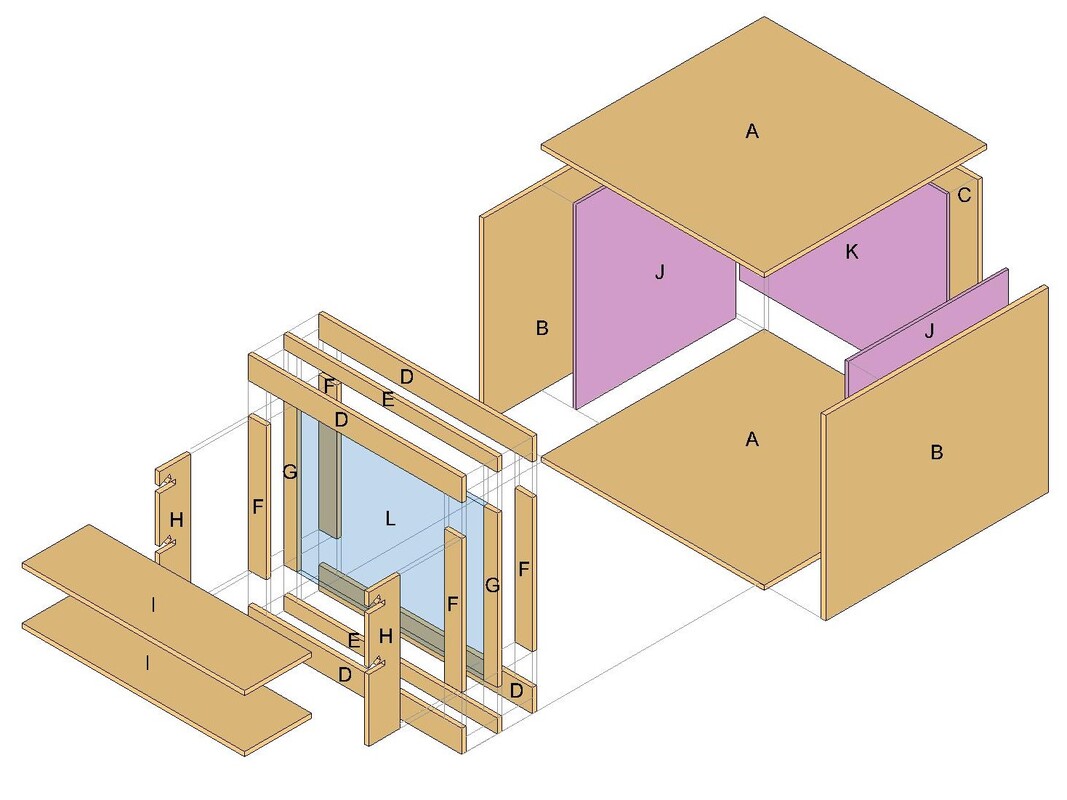
Exploded View

3d Rendered Views

CNC cutouts

CNC for Internal DHT sensor

CNC for External sensor

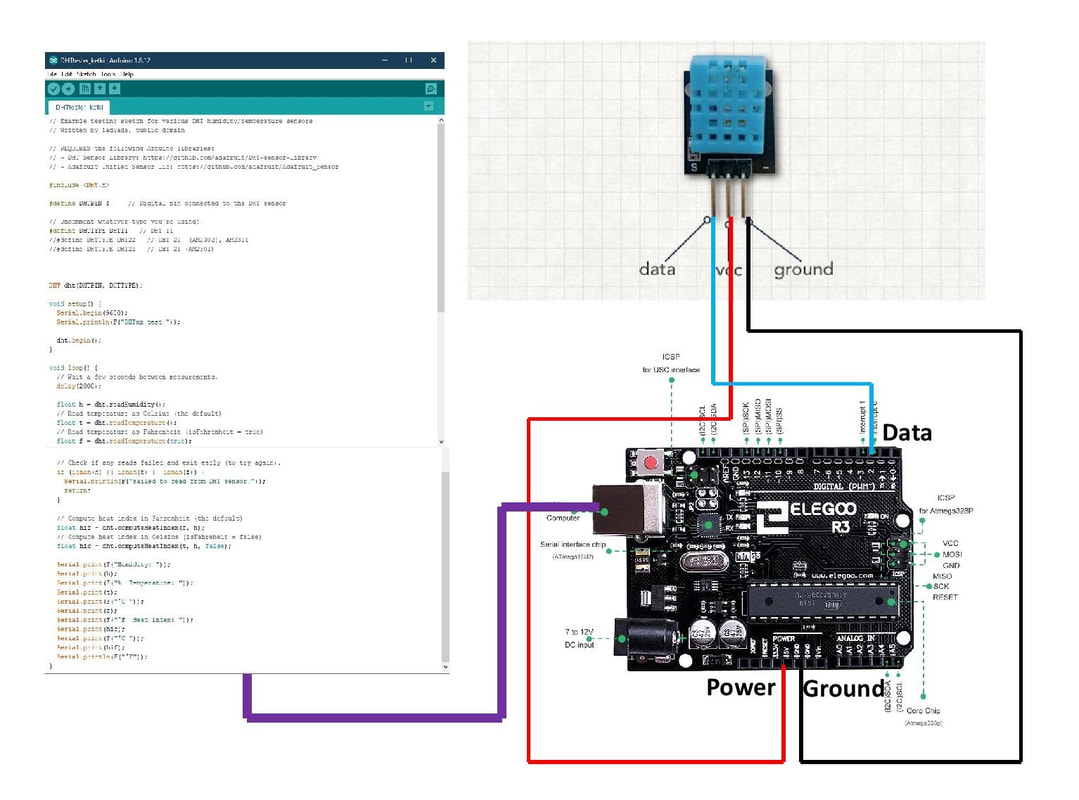
Electronics Connections

Arduino Code


    












Electronic Component required:
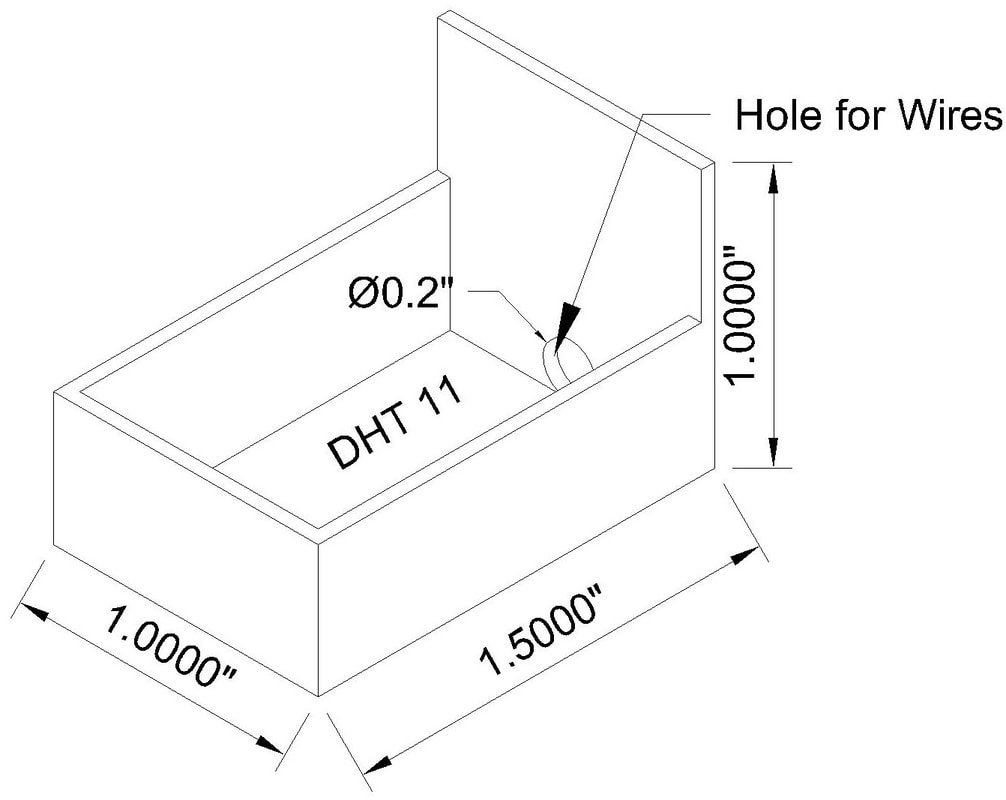
Temperature and Humidity Sensor (DHT11)
Arduino Uno
3 M-F wires
USB cable

Software:
Arduino IDE