Balance Point Game
Rules
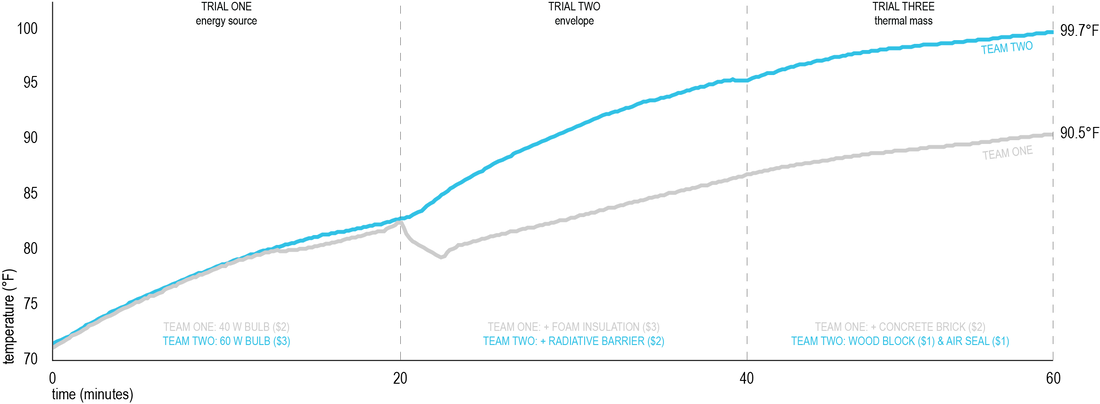
The goal is to raise the equilibrium temperature of the cube. However, improvements must be added and evaluated one at a time (every 20 minutes). After each improvement is added, the group will monitor the cube’s temperature to gauge the effect of the improvement. Groups will record improvements, times, and temperatures on the evaluation forms provided, and on a master graph for the class. Rules:
• One glass side of the cube must always remain uncovered.
• The wood base of the cube must remain on the bottom.
• No material may be added to the interior of the cube except a new light bulb, a block of mass, or a can.
• No modifications are allowed which attempt to specifically influence the local area of the thermometer in an unrepresentative way.
• Prohibited activities will result in bankruptcy and disqualification.
Groups will be billed for energy at the rate of $2/Wh.
• 25W bulb for 20 minutes = 8.25 Wh ($16.00)
• 40W bulb for 20 minutes = 13.2 Wh ($26.00)
• 60W bulb for 20 minutes = 18 Wh ($36.00)
Students are encouraged to spend as little as possible - prices assigned to the improvements are just a device and do not represent real market values. Each group will have a budget of $100. Potential Improvements:
• One glass side of the cube must always remain uncovered.
• The wood base of the cube must remain on the bottom.
• No material may be added to the interior of the cube except a new light bulb, a block of mass, or a can.
• No modifications are allowed which attempt to specifically influence the local area of the thermometer in an unrepresentative way.
• Prohibited activities will result in bankruptcy and disqualification.
Groups will be billed for energy at the rate of $2/Wh.
• 25W bulb for 20 minutes = 8.25 Wh ($16.00)
• 40W bulb for 20 minutes = 13.2 Wh ($26.00)
• 60W bulb for 20 minutes = 18 Wh ($36.00)
Students are encouraged to spend as little as possible - prices assigned to the improvements are just a device and do not represent real market values. Each group will have a budget of $100. Potential Improvements:
Additional materials (for future games) might include: white / black paper or white / black / polished metal can
Background
Think about the internal gains in a building (ie all of the things that give off heat) - humans, lighting, equipment, appliances, computers, etc., etc. Now consider all of the external gains on a building - sunlight, wind, heat gain through infiltration, weather, etc.
The balance point is the base temperature necessary to anticipate annual energy demand to heat or cool a building (but NOT how you size a mechanical system). In other terms, it is the outdoor temperature where the energy produced in a space is equal to the energy escaping from the space (and the temperature remains steady). For example, if you set your thermostat to 65F and you have 5F of internal gains, your balance point = 60F.
To calculate this temperature, you first need to calculate the internal gains (how much "free heat" are you getting?). Next, you calculate the transmission loss through the envelope. ΔT = Q(int) / UA.
ΔT = change in temperature (°F or °C)
Q(int) = internal gains (BTU/hr)
UA = envelope losses: u-value x area (BTU/°Fhr)
The balance point is the base temperature necessary to anticipate annual energy demand to heat or cool a building (but NOT how you size a mechanical system). In other terms, it is the outdoor temperature where the energy produced in a space is equal to the energy escaping from the space (and the temperature remains steady). For example, if you set your thermostat to 65F and you have 5F of internal gains, your balance point = 60F.
To calculate this temperature, you first need to calculate the internal gains (how much "free heat" are you getting?). Next, you calculate the transmission loss through the envelope. ΔT = Q(int) / UA.
ΔT = change in temperature (°F or °C)
Q(int) = internal gains (BTU/hr)
UA = envelope losses: u-value x area (BTU/°Fhr)
1. Internal Gains
|
2. Transmission loss through envelope Solve for UAWhen specifying materials for buildings, we need to understand a materials capacity to transmit or resist heat flow (energy). This is typically described in R-value or U-value (inverse of R)
R-Value = the capacity of a material to resist heat flow (resistance value) (Ft2 °F hr / BTU) U-Value = the capacity of a material to transmit heat flow (BTU/Ft2 °F hr) |
Sample problem:
Find the balance point of a 30' x 40' x 10' house with R-10 walls, floor and ceiling. There are 4 people (300 btu/hr) and (10) 40 W lights.
1. calculate internal loads: (remember, 1W = 3.41 BTU/hr)
4 x 300 BTU/hr (people) + 10(40 W) x 3.41 BTU/W = 1200 BTU/hr + 1364 BTU/hr = 2564 BTU/hr = Q(int) (internal gains)
2. calculate transmission loss (find UA)
2 (40 x 10') = 800 ft2 (long wall)
2 (30 x 10') = 600 ft2 (short wall)
2 (30 x 40') = 2400 ft (floor and ceiling) =3800 ft2 = A (area)
3800 ft2 x (1/10 Btu/ft2Fhr) = 380 BTU/Fhr = UA (transmission loss)
3. Find ΔT assuming the outside temperature is 65F
ΔT = Q(int) / UA. So... (2564 BTU/hr) / (380 BTU/Fhr) = 6.75 F.
So that means that you're getting 6.75 F of gains and when it's 65F outside, your temperature will balance out at 71.75F.
1. calculate internal loads: (remember, 1W = 3.41 BTU/hr)
4 x 300 BTU/hr (people) + 10(40 W) x 3.41 BTU/W = 1200 BTU/hr + 1364 BTU/hr = 2564 BTU/hr = Q(int) (internal gains)
2. calculate transmission loss (find UA)
2 (40 x 10') = 800 ft2 (long wall)
2 (30 x 10') = 600 ft2 (short wall)
2 (30 x 40') = 2400 ft (floor and ceiling) =3800 ft2 = A (area)
3800 ft2 x (1/10 Btu/ft2Fhr) = 380 BTU/Fhr = UA (transmission loss)
3. Find ΔT assuming the outside temperature is 65F
ΔT = Q(int) / UA. So... (2564 BTU/hr) / (380 BTU/Fhr) = 6.75 F.
So that means that you're getting 6.75 F of gains and when it's 65F outside, your temperature will balance out at 71.75F.
With your team...
|
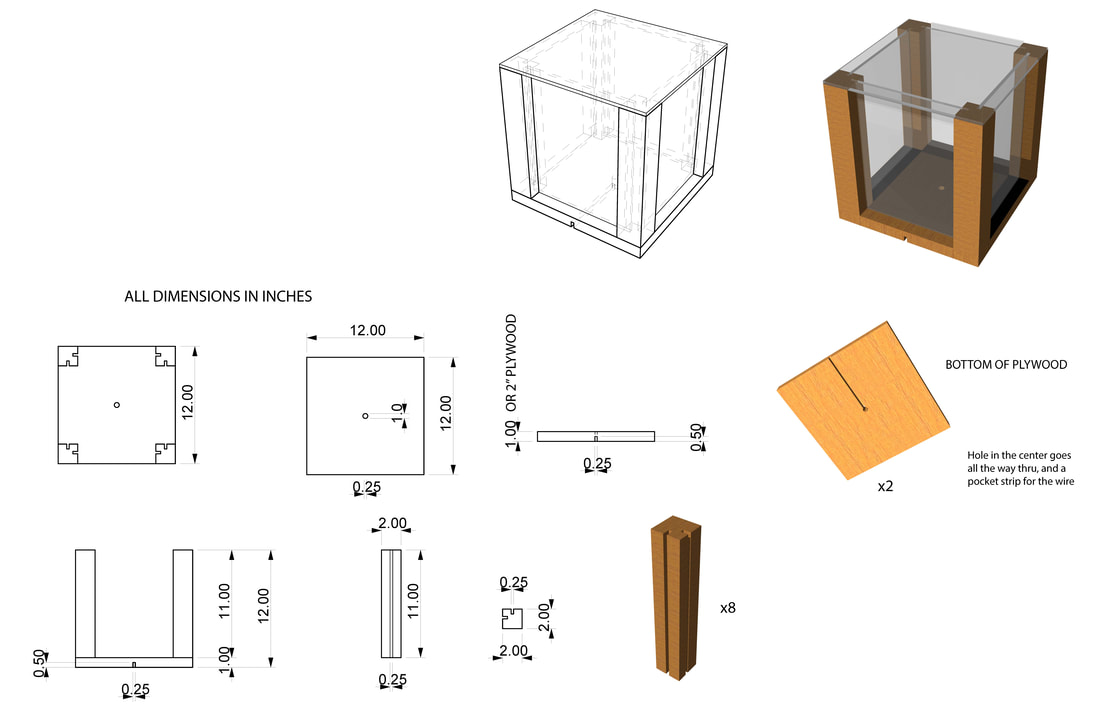
Predict the temperature inside the box after 20 minutes. Assume that the room temperature is 70 degrees. Assumptions: The box is 11" x 11" x 11" (for simplicity, you may assume that it is 1' x 1' x 1'). The (4) walls and (1) roof are 1/4" acrylic with an R-value of .86 (Ft2 °F hr / BTU). The base is MDF, which has an R-value of 2.35 (Ft2 °F hr / BTU). Finally, decide your next 'investment' - would it be more effective to improve the envelope (minimize losses) or add energy (increase interior gains)? |